Aliasing, Anti-aliasing – What is that anyway?
Tech Note
All Dataforth analog input products feature a front end filter. This note explains one of the reasons why.
 In electronics it’s not about changing a name, but it is about the very gross distortions that can happen in sampled data signal processing. To keep it simple, consider an analog to digital converter (ADC) and processor sampling a pure sine wave. Sweep the sine wave frequency from very low to slightly higher than the system sample rate. At frequencies many times lower than the sample rate, the signal will be sampled many times per cycle. Any interpretation of the sampled data will yield a good approximation to the actual signal. As the pure sine wave frequency approaches the sample rate, any interpretation of the data is surely going to be a very poor representation of the sine wave signal. Keep in mind that low frequency complex waveforms are composed of higher frequency, sine wave harmonics.
In electronics it’s not about changing a name, but it is about the very gross distortions that can happen in sampled data signal processing. To keep it simple, consider an analog to digital converter (ADC) and processor sampling a pure sine wave. Sweep the sine wave frequency from very low to slightly higher than the system sample rate. At frequencies many times lower than the sample rate, the signal will be sampled many times per cycle. Any interpretation of the sampled data will yield a good approximation to the actual signal. As the pure sine wave frequency approaches the sample rate, any interpretation of the data is surely going to be a very poor representation of the sine wave signal. Keep in mind that low frequency complex waveforms are composed of higher frequency, sine wave harmonics.
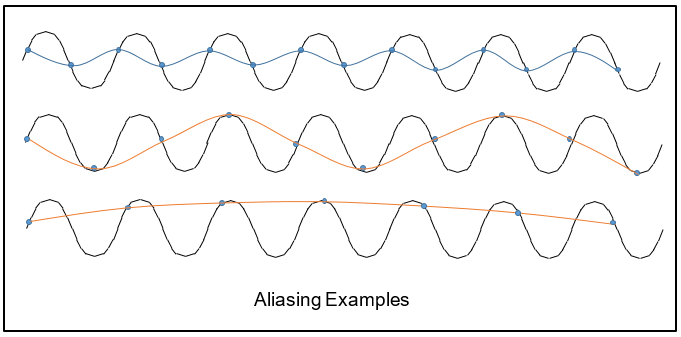
Consider the top wave form of the figure. The sine wave is being sampled twice per period. The sampling frequency is twice that of the signal. The data samples represent a very poor interpretation of the signal, but they do have one piece of true intelligence. They do correctly represent the period of the signal. This represents, however crudely, the famous Nyquist-Shannon theorem. If a complex wave form has no frequencies greater than fmax(Hz), it should be sampled at least every 1/(2fmax) seconds.
Now sample a little more slowly. The middle signal is sampled about every 3/2 of the signal period. Any interpretation of those samples is certainly not the signal. We might infer a period, but it would clearly be a much longer period than the actual signal. You might say, we have lost intelligence about the signal. The signal has been aliased to a lower frequency, a false frequency.
The bottom sampled signal is sampled less than once per period, and any inferred period is shifted even longer than the middle shifted signal.
If we are dealing with complex wave forms, not pure sine waves, the plot thickens. We know from Fourier Transform theory that complex wave forms are composed of a series of sine waves of increasing, harmonic frequency.
The common practice is to put a low pass filter in front of the sampled data system. This prevents any frequencies greater than one half the sample rate from entering. Hence the name anti-aliasing. The filter is called an anti-aliasing filter. Who would have guessed?
Actually, since low pass filters only attenuate, not zero, higher frequencies, the usual practice is to sample more than just twice the frequency of the highest signal frequency component. Sometimes a small amount, or depending on the application and quality of the low pass filter, many times higher. Much more about this can be found in Dataforth application note AN115, Data Acquisition and Control Sampling Law.
For further and deeper reading, search Wikipedia for "Anti-aliasing filter." In that article and the references therein, you will find more than you may want to know, including heavy mathematics. Another good search is "Nyquist-Shannon sampling theorem." Nobel Prize level stuff. Shannon did receive the Alfred Noble prize. No, not the same prize. Claude Shannon built on the prior work of Harry Nyquist.
Another pitfall in practical systems is signal clipping. If a signal level is too high, it may be clipped at a signal flow point beyond the filter. Not only is the signal clipped, but high frequency harmonics are introduced causing aliasing.






