an113: Phase Angles and Time Delays
Application Note
Preamble
As a prerequisite to this Application Note, the reader is encouraged to examine Dataforth’s Application Note AN112, Reference 2, which describes the amplitude characteristics and reviews the analytical techniques of low-pass filter frequency dependent transfer functions associated with Dataforth’s signal conditioning modules’ filter circuits.Internal filtering enhances sensor signal integrity of signal conditioning modules (SCM) by eliminating undesirable frequency and noise components. However, the inherent characteristic of this type of filtering functionality adds a phase angle with an associated propagation delay to the original signal. This added phase and delay does not generally affect steady state low frequency industrial process measurements. However, in some situations, near instantaneous changes in process variables need instant recognition. In these situations, one should carefully examine SCM specifications to determine their applicability. Dataforth SCM specifications include pulse transient data to assist selection. Visit Dataforth’s website, Reference 1.
The objective of this application note is to present a brief visual examination of typical SCM low-pass (LP) filter pulse and phase characteristics. For simplicity, only RC low-pass filters are examined, with a minimum of mathematical analysis, to establish some general firstorder- approximation conclusions. Multi-pole filter characteristics can be created by cascading the topologies illustrated in Figures 1, 2, and 3. In practice, circuit values are adjusted to create special amplitude, phase, and pulse characteristics. Years of research on filter topologies such as Bessel, Butterworth, Chebyshev, Cauer, etc., have established standard filter characteristics with associated component selection rules. The interested reader is encouraged to examine the exhaustive literature on these characteristics.
Low-Pass RC Filters
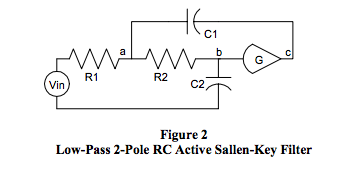
Figures 1 and 2 illustrate two different low-pass 2-pole RC filter topologies, which are examined here to develop an understanding of low-pass filter phase shift and delay characteristics. In Figure 1, the RC sections are isolated by a unity gain amplifier, which is not necessary but is included here for illustration purposes.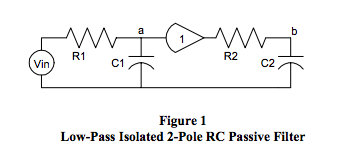
Equation 1 describes the steady state sinusoidal s-domain transfer function format for a typical low-pass 2-pole RC filter. The “b” coefficients of “s” in the denominator, D(s), determine the filter poles and are functions of RC component values. See Reference 2.
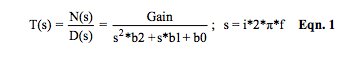
Coefficients b2 and b0 are defined as b2 = C1*R1*C2*R2 and b0 = 1. However, coefficient b1 has different values dependent on the circuit topology. Expressions for b1 are:
-
- Figure 1: Isolated RC sections, Gain = 1
b1 = C1*R1 + C2*R2, (gain independent)
- Figure 1: Interacting RC sections, No amplifier
b1 = C1*R1 + C2*(R1+R2)
- Figure 2: Active RC Sections
b1 = C1*R1*(1-G) + C2*(R1+R2)
The typical analysis of frequency dependent transfer functions, N(s)/D(s), determines the relationship between denominator, D(s), roots defined as poles, and numerator, N(s), roots defined as zeros. Historically, the analysis of transfer function characteristics uses the locations of poles in the s-plane to establish a multitude of well-known specific behavior characteristics such as the Bessel, Butterworth, Chebyshev, and Cauer, which provide designers with the opportunity to tailor filter behavior to specific applications. Complete in-depth reviews of this information are beyond our objective for this document.
A practical examination of RC low-pass filter pulse response and phase shift characteristics, primarily focused on LP type filters necessary in industrial signal conditioning modules, will now be presented. Examination of the typical transfer function for a lowpass 2-pole RC filter topology as expressed in Equation 1, where N(s) is a constant (the Gain), illustrates some basic LP filter behavior characteristics.
1. RC products are recognized as time-constants “τ ” and their reciprocals “1/τ ” have units of radians per second “ω ” where ω = 2*π *f, and “f” is frequency, in Hertz.
2. Equations 2, 2a, and 3 are illustrations of how Equation 1 can be rewritten. Recall that “roots” are the mathematical solutions of D(s) = 0 and are the reciprocal of filter time constants.
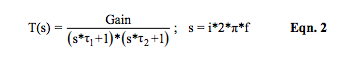
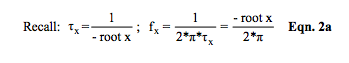
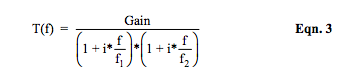
3. Roots of D(s), the dominator, are often referred to as poles. Their values are determined by the coefficients b2, b1, and b0, which are determined by circuit RC values. These roots control LP filter behavior with respect to frequency. Equation 3 illustrates the frequency dependent complex filter transfer function, T(f), of Equation 1 in terms of f1 and f2 , which are roots of D(s) divided by 2*π . Equation 4 shows the typical case for “n” denominator roots of a low-pass filter transfer function where f1 , f2 , … fn are defined as “break point” frequencies. When roots are complex numbers, equations and associated mathematics become very complicated.
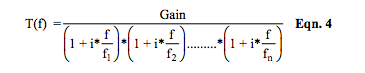
4. Magnitude and phase response as a function of frequency can be determined from Equations 3 and 4. The pulse response as a function of time is extremely important in determining filter delays and response times. Equation 5 describes the one-volt step input time response of the typical low-pass 2-pole RC filter of Equation 2 with non-repeating real denominator roots.
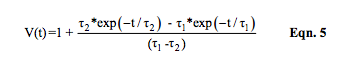
Recall that the time constants in Equations 2 and 5 are negative reciprocals of denominator roots in Equation 1.
Historically, most texts on filters analyze behavior with respect to the number of poles, their position relative to one another, and their position in the s-plane. Manually calculating poles requires knowledge of the “b” coefficients of D(s) and methods of finding roots of multidimensional polynomials, which can be a very difficult task. Special simulation software simplifies this task. There are some simple circuit observations one can use to get a “feel” for the basic behavior of RC low-pass SCM filters. The best way to explore these simple approximations is to examine some visual examples using the low-pass RC 3-pole filter in Figure 3.
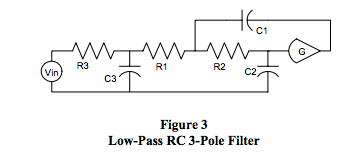
Equations 6 and 6a represent the s-domain transfer function of Figure 3.
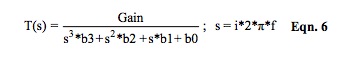
Equation 6 can be arranged in the following form:
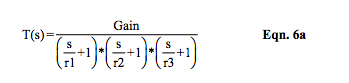
Recall that circuit values determine the “b” values and these “b” values uniquely determine the denominator’s mathematical roots, which are the “r” values in Equation 6a. Dataforth design engineers select circuit values, which establish different sets of “b” values. These “b” values determine the filter poles, which uniquely establish filter behavior.
Mathematically, the denominator roots of filter transfer functions, T(s), can be real numbers or complex numbers (x + i*y) or a combination. In addition, mathematically calculated roots must be entered in factored equations like Equation 6a as negative values. Note: If the real part of any root of D(s) is (or ever can become) positive, the filter is unstable. Readers may want to review feedback theory to explore the phenomena of stability.
The following list and associated Table 1 shown below outline some different root possibilities for the filter circuit in Figure 3.
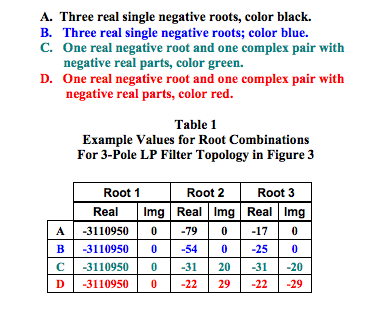
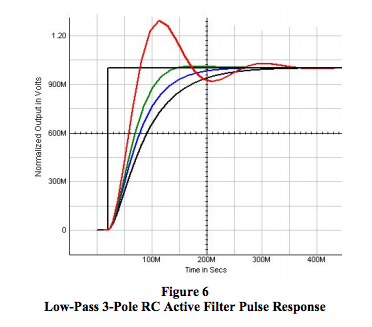
Figures 4, 5, and 6 illustrate how the example categories of “roots” in Table 1 affect low-pass filter behavior of the circuit shown in Figure 3. The curves in these figures are color coded to agree with Table 1. There are an infinite number of possible combinations of circuit values. Hundreds of articles and scores of texts have been written with rigorous mathematical treatment on how to select circuit values to achieve specific filter behavior such as Bessel, Butterworth, and Chebyshev, to mention a few.
Figures 4 and 5 illustrate how the roots of D(s) affect amplitude and phase response versus frequency of the filter topology in Figure 3.
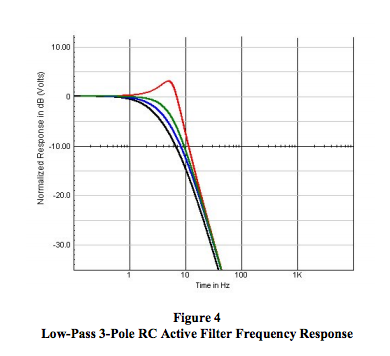
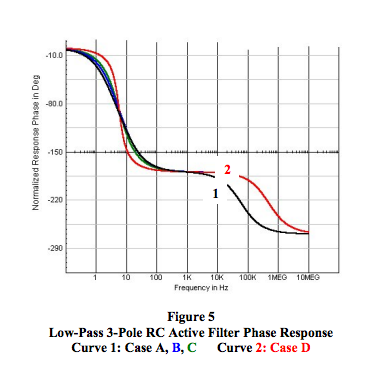
Figure 6 shows the response to a unit step input. Of particular interest is the graphical relationship between frequency response and step input pulse response.
General Observations
The following are some general observations and relationships relative to basic LP filters used in signal conditioning modules. For simplicity, rigorous mathematical analysis and proofs are omitted.1. For LP filters, the upper 3dB frequency is determined by the interaction between all the filter poles. If there is one dominant pole (smaller by a factor of 5-10), then it is primarily responsible for the upper 3dB frequency. See Reference 2 and Equation 4. Note: The number of poles equals the number of time-constant capacitors in an RC low-pass filter.
2. The frequency dependent phase shift behavior of stable low-pass RC filters is a composite combination of the phase shift contribution of each pole/root of D(s). Each pole can contribute up to 90 degrees of negative phase shift as frequency increases. For example, a 3-pole RC LP filter can have a maximum of 270 degrees of negative phase shift. The exact shape of a phase versus frequency plot is dependent upon the specific root values of D(s). See Figure 5.
3. As Figure 6 illustrates, the step input response has a time dependent behavior, which is very sensitive to the specific root values of D(s).
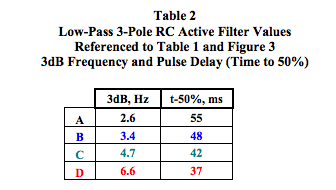
4. As the “real” part of roots gets smaller with the “imaginary” part simultaneously increasing, the frequency response begins to peak near the 3dB frequency and the step response tends toward ringing. Examine Case C (green) and Case D (red) in Tables 1 and 2 and Figures 4, 5, and 6. Clearly, both the 3dB frequency and the filter response time are tightly coupled and totally controlled by the roots of D(s), which are subject to the “b” coefficients as determined by RC values and filter gain. Changing circuit values to achieve a specific frequency behavior will affect the pulse response and vice versa.
Industrial SCMs require internal multiple-pole LP filtering that has: (a) specified 3dB frequency, (b) steep attenuation well above the 3dB frequency (20dB per pole per frequency decade), (c) flat response with minimum ringing or ripples within the pass-band, and (d) antialiasing function on the field side prior to amplification. Dataforth design engineers use rigorous design tools to provide all of these multi-pole SCM filter characteristics. The reader is encouraged to visit Reference 1 and examine Dataforth’s full line of SCMs and their associated filter characteristics.
More for the Interested Reader
Dataforth has an interactive Excel workbook for a 2-pole RC active LP filter. This Excel workbook allows one to enter individual circuit values and obtain instant plots for Step Input Responses, Gain versus Frequency, and Phase versus Frequency. Readers interested in exploring how circuit values influence filter poles, which in turn determine filter behavior, are encouraged to download this Excel file; see Reference 3.
Dataforth References
- Dataforth Corp. Website
http://www.dataforth.com - Dataforth Corp., Application Note AN112
Filtering in Signal Conditioning Modules - Dataforth Corp. Excel Interactive Workbook
for 2-Pole LP Active Filter
Interactive Workbook for 2-Pole LP Active Filter
Was this content helpful?
Thank you for your feedback!






