an123: Tuning Control Loops for Fast Response
Application Note
Preamble
The Cohen-Coon tuning rules work well on virtually all self-regulating processes. These rules were originally designed to give a very fast response, but this results in loops with a very oscillatory response. With a slight modification of the Cohen-Coon tuning rules, control loops can still respond quickly, but they are much less prone to oscillations. This Application Note describes how to tune control loops using this modified CohenCoon tuning method.Applicable Process Types
The Cohen-Coon tuning method can be used only on selfregulating processes. Most control loops, e.g., flow, temperature, pressure, speed, and composition, contain self-regulating processes. The most common exception is a level control loop, which contains an integrating process.A self-regulating process always stabilizes at some point of equilibrium, which depends on the process design and the controller output. If the controller output is set to a different value, the process will respond and stabilize at a new point of equilibrium.
Target Controller Algorithm
The Cohen-Coon tuning rules have been designed for use on a noninteractive controller algorithm such as that provided by the Dataforth MAQ® 20 system.Procedure
To apply the modified Cohen-Coon tuning rules, follow the steps below. The process variable and controller output must be time-trended so that measurements can be taken from them.- Do a controller output step test:
- Put the controller in manual and wait for the process to settle out.
- Make a step change in the controller output (CO) of a few percent and wait for the process variable (PV) to settle out. The size of this step should be large enough that the PV moves well clear of the process noise/disturbance level. A total movement of five times more than the peak-to-peak level of the noise and disturbances on the PV should be sufficient.
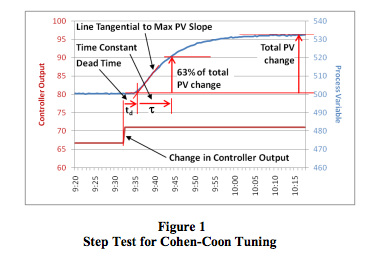
- Determine the process characteristics (refer to Figure 1):
- If the PV is not ranged 0-100%, convert the
change in PV to a percentage of the range as
follows:
Change in PV [in %] = change in PV [in Eng. Units] × 100 / (PV upper calibration limit - PV lower calibration limit) - Calculate the Process Gain (gp):
gp = total change in PV [in %] / change in CO [in %] - Find the maximum slope of the PV response curve. This will be at the point of inflection. Draw a tangential line through the PV response curve at this point.
- Extend this line to intersect with the original level of the PV before the step in CO.
- Take note of the time value at this intersection
and calculate the Dead Time (td):
td = time difference between the change in CO and the intersection of the tangential line and the original PV level - If td was measured in seconds, divide it by 60 to convert it to minutes. Since the Dataforth PID controller uses minutes as its time base for integral time, all measurements have to be made in minutes or converted to minutes.
- Calculate the value of the PV at 63% of its total change.
- On the PV reaction curve, find the time value at which the PV reaches this level.
- Calculate the Time Constant (τ):
τ = time difference between intersection at the end of dead time and the PV reaching 63% of its total change - If τ was measured in seconds, divide it by 60 to convert it to minutes.
- Repeat steps 1 and 2 three more times to obtain good average values for the process characteristics.
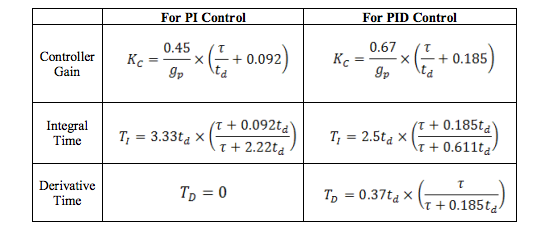
- Calculate controller settings for a PI or PID controller using the modified Cohen-Coon equations below. (The modified rules calculate the controller gain as ½ of that calculated by the original rules.)
- Enter the values into the controller, make sure the algorithm is set to Noninteractive, and put the controller in automatic mode.
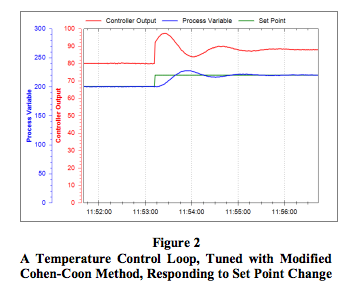
- Change the set point to test the new values.
- Do fine tuning if necessary. The control loop’s response can be slowed down and made less oscillatory, if needed, by decreasing Kc and/or increasing Ti.
Conclusion
While the Ziegler-Nichols tuning method does not work well on all self-regulating processes, the modified CohenCoon tuning rules provide a good alternative for achieving fast response on virtually all control loops with self-regulating processes.References
[1] G.H. Cohen and G.A. Coon, Theoretical Consideration of Retarded Control, Trans. ASME, 75, pp. 827-834, 1953.The reader is encouraged to visit Dataforth’s website to learn more about PID control and the MAQ®20.
- Application Note 122: Introduction to PID Control http://www.dataforth.com/catalog/pdf/AN122.pdf
- MAQ® 20 Brochure http://www.dataforth.com/catalog/pdf/MAQ20_broch ure.pdf
Was this content helpful?
Thank you for your feedback!






