an125: Tuning Level Control Loops

Preamble

The original Ziegler-Nichols tuning methods published in 1942 aimed for a super-fast speed of response at the expense of control loop stability. However, with a slight modification of their tuning rules, the loop stability can be improved. This comes at the expense of a slight reduction in the speed at which a control loop responds to a disturbance or set point change. However, most process experts will agree that control loop stability is more important than speed. This Application Note describes how to tune level control loops using this modified Ziegler-Nichols tuning method.

Applicable Process Types

The tuning method described below is intended for use with integrating processes. Level control loops (Figure 1) are the most common example of loops containing integrating processes.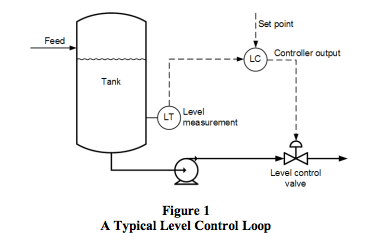



An integrating process will stabilize at only one controller output, the point of equilibrium. If the controller output is set to a different value, the process will increase or decrease indefinitely at a steady slope (Figure 2).



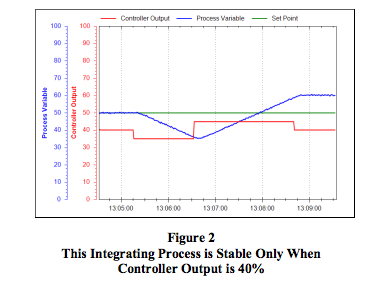
It should also be noted here that this tuning rule provides a fast response to disturbances in level and is therefore not suitable for tuning level control loops for surge tanks.

Target Controller Algorithm

The modified Ziegler-Nichols tuning rules presented here are designed for use on a noninteractive controller algorithm with its integral time set in minutes, such as the one provided in the Dataforth MAQ^® 20 system.

Procedure

To apply these tuning rules for an integrating process, follow the steps below. The process variable and controller output must be time-trended so that measurements can be taken from them (Figure 3).

1. Do a step test:
   1. Make sure, as far as possible, that the uncontrolled flow into/out of the vessel is as constant as possible.
   2. Put the controller in manual control mode.
   3. Wait for a steady slope in the level. If the level is very volatile, wait long enough to be able to confidently draw a straight line though the general slope of the level.
   4. Make a step change in the controller output. Try to make the step change 5% to 10% in size, if the process can tolerate it.
   5. Wait for the level to change its slope into a new direction. If the level is volatile, wait long enough to be able to confidently draw a straight line though the general slope of the level.
   6. Restore the level to an acceptable operating point and place the controller back in auto control mode.
2. Determine the process characteristics (refer to Figure 3):
   1. Draw a line (Slope 1) through the initial slope, and extend it to the right as shown in Figure 3.
   2. Draw a line (Slope 2) through the final slope, and extend it to the left to intersect Slope 1.
   3. Measure the time between the beginning of the change in controller output and the intersection between Slope 1 and Slope 2. This is the process dead time (td), the first parameter required for tuning the controller.
   4. If td was measured in seconds, divide it by 60 to convert it to minutes. Since the Dataforth PID controller uses minutes as its time base for integral time, all measurements have to be made in minutes.
   5. Pick any two points (PV1 and PV2) on Slope 1, located conveniently far from each other to make accurate measurements.
   6. Pick any two points (PV3 and PV4) on Slope 2, located conveniently far from each other to make accurate measurements.
   7. Calculate the difference in the two slopes (DS) as follows: DS = (PV4 - PV3) / T2 - (PV2 - PV1) / T1 Note 1: If T1 and T2 measurements were made in seconds, divide them by 60 to convert them to minutes.
   8. If the PV is not ranged 0-100%, convert DS to a percentage of the range as follows: DS% = 100 × DS / (PV range max - PV range min)
   9. Calculate the process integration rate (ri), which is the second parameter needed for tuning the controller: ri = DS [in %] / dCO [in %]
   
   
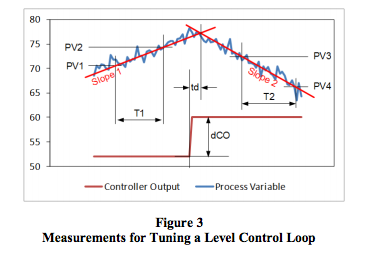
3. Repeat steps 1 and 2 three more times to obtain good average values for the process characteristics t_d and r_i.
4. Calculate tuning constants:
   
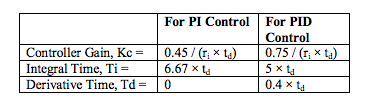
   Note that these tuning equations look different from the commonly published Ziegler-Nichols equations. The first reason is that the Kc has been reduced and Ti increased by a factor of 2, to make the loop more stable and less oscillatory. The second reason is that the Ziegler-Nichols equations for PID control target an interactive controller algorithm, while the Dataforth MAQ^®20 has a noninteractive algorithm. The PID equations above have been adjusted to compensate for the difference.
5. Enter the values into the controller, make sure the algorithm is set to Noninteractive, and put the controller in automatic mode.
6. Change the set point to test the new values.
7. Do fine tuning if necessary. For integrating processes, Kc and Ti need to be adjusted simultaneously, and in opposite directions. For example, to slow down the control loop, use Kc / 2 and Ti × 2.
   
   

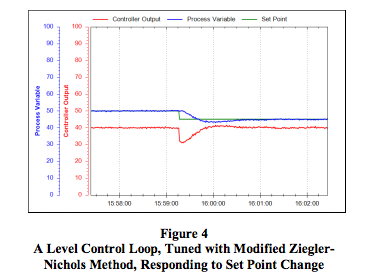
Conclusion

With a few modifications to the original Ziegler-Nichols tuning rules, these rules can be used to tune level control loops for a fast response to set point changes and disturbances.

References

[1] J.G. Ziegler and N.B. Nichols, Optimum settings for automatic controllers, Transactions of the ASME, 64, pp. 759–768, 1942

The reader is encouraged to visit Dataforth’s website to learn more about PID control and the MAQ^®20.

1. Application Note 122: Introduction to PID Control
   http://www.dataforth.com/catalog/pdf/AN122.pdf
2. MAQ^®20 Brochure
   http://www.dataforth.com/catalog/pdf/MAQ20_broch ure.pdf